[Machine Learning] Linear Models_Part 1

<Introduction>

선형 모델은 지난 몇십년간 넓게 연구되었고, 실전에서 자주 사용하는 모델이다.

선형 모델은 입력된 데이터에 대한 선형 함수를 사용하여 데이터들을 예측하는 역할을 한다. 

---

<Linear models for Regression>

일반적으로 회귀에서 사용되는 모델은 해당 공식을 따른다.

다중 선형 방정식

여기서 보이는 x[0]부터 x[p]는 개별적 데이터에 대한 특징을 나타내고, w와 b는 모델에서 학습되는 파라미터이다. 그리고 ŷ는 모델이 예측한 값을 나타낸다. 만약 데이터 셋이 하나의 특징만을 가진다면 아래 방정식을 따른다.

단일 선형 방정식

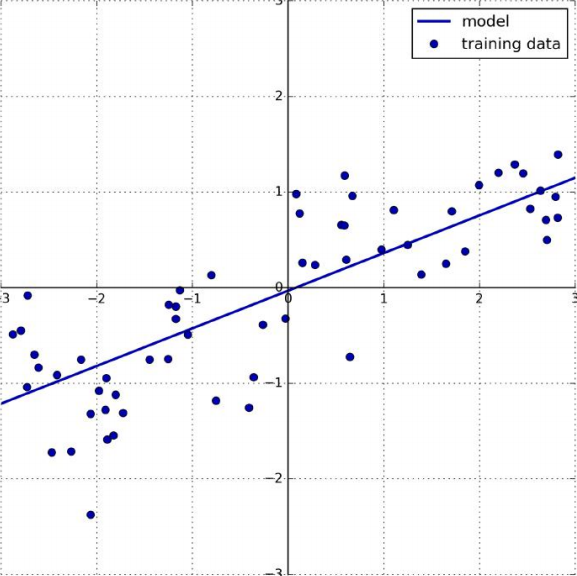
위에 보이는 그래프는 일반적인 단일 선형 방정식의 기본적인 형태이다. 

---

<Linear Regression>

선형 회귀는 간단하고, 회귀에서 가장 기본적인 방법이다. 선형 회귀는 w와 b의 값을 예측값과 타겟 데이터의 값에 평균 제곱 오차의 값을 줄이기 위해 찾는다. 평균 오차 제곱은 예측한 값과 타겟 데이터의 값의 차를 제곱해주고, 전체 개수로 나눠준다. 선형 회귀는 파라미터가 없는데, 이로써 모델의 복잡성이 떨어진다.

data = pd.read_csv('/kaggle/input/random-linear-regression/test.csv').to_numpy()
x = data[:, 0].reshape(-1, 1)
y = data[:, 1].reshape(-1, 1)
train_input, test_input, train_target, test_target = train_test_split(x, y, test_size=0.3)

fig, ax = plt.subplots(ncols=2, figsize=(10, 4))
ax[0].scatter(train_input, train_target, label='train dataset', marker='x', color='Orange')
ax[1].scatter(test_input, test_target, label='test dataset', marker='X', color='violet')
ax[0].legend()
ax[1].legend()

lr = LinearRegression()
lr.fit(train_input, train_target)
print('train dataset = {}\n'.format(lr.score(train_input, train_target)))
print('test dataset = {}\n'.format(lr.score(test_input, test_target)))
print('w = {}, b = {}\n'.format(lr.coef_, lr.intercept_))

fig, ax = plt.subplots(ncols=3, figsize=(15, 4))
ax[0].scatter(train_input, train_target, marker='x', label='train dataset', color='Orange')
ax[1].scatter(test_input, test_target, marker='X', label='test dataset', color='violet')
ax[2].plot(x, lr.coef_*x + lr.intercept_, label='graph', color='Red')
ax[0].legend()
ax[1].legend()
ax[2].legend()

fig, ax = plt.subplots()
ax.scatter(train_input, train_target, marker='x', label='train dataset', color='Orange')
ax.scatter(test_input, test_target, marker='X', label='test dataset', color='violet')
ax.plot(x, lr.coef_*x + lr.intercept_, label='graph', color='red')
ax.legend()

---

다음 예제를 살펴보자

X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
print('Train score : {}\n'.format(lr.score(X_train, y_train)))
print('Test score : {}\n'.format(lr.score(X_test, y_test)))

다음과 같이 오버피팅이 발생하는 것을 볼 수 있다. 이러한 경우에는 어떻게 해야 할까? 오버피팅이 되었다는 것은 해당 데이터의 값에 너무 과하게 맞춰 있다는 뜻이기 때문에 모델에 복잡성을 줘서 이러한 점을 조금 풀어줘야 한다. 이에 대한 대안으로 ridge regression을 써 볼것이다.