[Machine Learning] K-NN Algorithms
앞선 글에서 K-NN Algorithms이라는 알고리즘에 대해서 설명하였다.
저번시간에는 K-NN Algorithms에 대해서 간단히 살펴보았다면 이번에는 K-NN Algorithms의 세부적인 사항까지 분석해보는 시간을 갖겠다.
<K-NN의 동작 원리>
1. 유클리드 거리계산법
유클리드 거리는 우리가 어렸을 때 배웠던 피타고라스의 정리와 비슷한 개념을 이용한 것이다. 피타고라스의 정리는 이미 만들어진 삼각형을 이용하여 빗변을 구하거나 다른 변을 구하는 반면에, 유클리드 거리 계산이란 해당 지점을 삼각형으로 만들어 계산한다는 것이다.
해당 세 좌표에 값이 주어질 때 해당 거리를 구해주면 된다. D의 값의 경우 피타고라스의 정리에 의해서

위와 같은 식으로 구할 수 있다. 만약 2차원이 아닌 3차원 좌표에 있을 경우에는

과 같은 방식으로 풀어주면 된다.
2. 맨해튼 거리

다음과 같이 한 지점에 가기 위해서 여러개의 길이 존재할 수 있는데, 초록색 선은 유클리드 거리로 선을 그은 것이다. 좌측 아래가 출발점이고 우측 상단이 도착점이라고 보았을 때 상식적으로 초록색으로는 이동할 수 없다. 건물과 건물 사이를 저렇게 통과할 수는 없기 때문이다. 여기서의 함정은 대부분의 사람들이 초록색 선과 가장 가까운 파란색 선이 출발점에서 도착점까지 도착할 수 있는 최단거리라고 생각한다는 것인데, 빨간색, 파란색, 노란색 선 모두 동일한 길이를 가진다는 것이 바로 핵심이다. 따라서 출발점의 좌표를 (x1, y1) 이라 하고, 도착점의 좌표를 (x2, y2)라고 할 때

위와 같은 공식이 나온다.

따라서 우리는 맨해튼 거리의 공식을 위와 같이 정의내릴 수 있게 된다.
3. 변수 값 범위 재조정
내가 저번에 올렸던 데이터의 경우

위와 같이 생긴것을 볼 수 있다. Height의 경우 158부터 170까지 총 x의 길이는 12이고, Weight의 경우 58부터 68까지 y의 길이는 10인것을 볼 수 있다. x의 길이와 y의 길이가 다른 것을 알 수 있는데 지금은 데이터의 구간이 별로 크지 않기 때문에 별 문제가 생기지 않았지만, 만약 몸무게가 58부터 100까지로 데이터가 늘어난다면 어떻게 될까? y의 값에 변화에 따라 타깃값이 많이 변하는 것을 볼 수 있을 것이다. 이를 예방하기 위해서 변수를 재조정하는 방법이 존재한다. 이 때 변수를 재조정 하는 것을 정규화라고 한다.
정규화를 하는 이유는 데이터가 가진 feature의 스케일이 심하게 차이가 나는 경우 문제가 되기 때문이다. 모든 데이터 포인트가 동일한 정도의 스케일(중요도)로 반영되도록 해주는게 정규화(Normalization)의 목표이다.
1) 최소-최대 정규화 (Min-Max Normalization)

예를 들어 주택에 관한 정보가 담긴 데이터를 생각해보자. 그 안에 특성으로 방의 개수(개), 얼마나 오래 전에 지어졌는지(년) 같은 것들이 포함될 수 있을거다. 그리고 여기서 머신러닝 알고리즘을 통해 어느 집이 가장 적합한지 예측을 시도한다고 해보자. 그러면 각 데이터 포인트를 비교할 때 더 큰 스케일을 가진 특성, 즉 얼마나 오래 전에 지어졌는지(년)에 따라 그 데이터가 완전히 좌지우지 되는 꼴이다. 우리는 머신러닝 알고리즘이 방 1개만 있는 집과 20개짜리 집이 얼마나 큰 차이가 나는지 인식하기를 기대한다. 이후 정규화 과정을 거치면 아래와 같이 바뀐다.

위와 같은 형태로 변화하게 된다.
최소-최대 정규화는 데이터를 정규화하는 가장 일반적인 방법이다. 모든 특성에 대해 각각의 최소값 0, 최대값 1로, 그리고 다른 값들은 0과 1 사이의 값으로 변환하는 거다. 예를 들어 어떤 특성의 최소값이 0이고 최대값이 100인 경우, 50은 딱 중간이므로 0.5로 변환된다.

하지만 이런 최소-최대 정규화에도 단점이 있는데, 이상치(outlier)에 너무 많은 영향을 받는다는 것이다. 예를 들어, 100개의 값이 있는데 그 중 99개는 0과 40 사이에 있고, 나머지 하나가 100이면 어떨까. 그러면 99개의 값이 모두 0부터 0.4 사이의 값으로 변환된다.
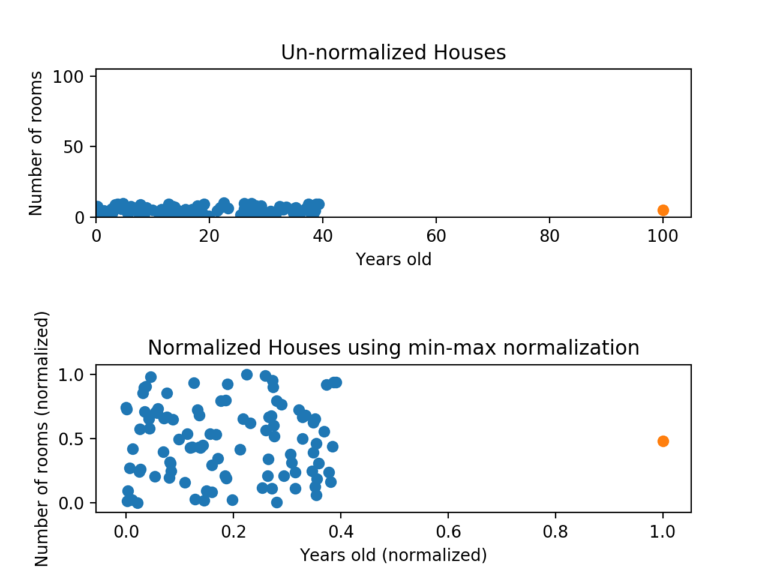
위 그림을 보면 y축에서는 정규화가 효과적으로 적용되었으나 x축에서는 여전히 잘못된 것을 알 수 있다. 데이터의 점들을 비교한다면, y축의 영향이 지배적일 수밖에 없다. 이러한 단점을 보완하려면 Z-점수 정규화를 고려해봐야 한다.
2) z-점수 표준화 (Z-Score Standardization)
Z-점수 정규화는 이상치(outlier) 문제를 피하는 데이터 정규화 전략이다. X라는 값을 Z-점수로 바꿔주는 식은 아래와 같다.

만약 특성의 값이 평균과 일치한다면 0으로 정규화되겠지만, 평균보다 작으면 음수, 평균보다 크면 양수로 나타난다. 이 때 계산되는 음수와 양수의 크기는 그 특성의 표준편차에 의해 결정되는 거다. 그래서 만약 데이터의 표준편차가 크면 (값이 넓게 퍼져있으면) 정규화 되는 값이 0에 가까워진다.

데이터가 여전히 찌그러져 보이긴 하지만, 그래도 거의 모든 점들이 x축과 y축에서 -2와 2 사이에 있다. 이제 어느정도 비슷한 스케일로 나타낸 셈이다. 여전히 x축에 5가 넘는 데이터 하나가 있어서 정확히 동일하진 않지만, 그래도 최소-최대 정규화에서 나타난 문제는 해결했다고 볼 수 있다.